A meritocracia é justa?
Esses tempos de autoverdades e de critérios individuais de racionalidade levaram-me a refletir se seria possível propor um método para um debate racional sobre aspectos mais subjetivos, como por exemplo, a meritocracia. Pelo fato de ter formação em Matemática, busquei pensar em algo próximo aos métodos matemáticos. Tentarei apresentar da maneira mais simples possível, mas peço que o leitor tenha um pouco mais de paciência na parte inicial do texto e não desista!
A matemática é uma ciência milenar. Existem registros encontrados sobre essa ciência que datam de mais de 2000 anos antes de Cristo. Pode-se dizer que o propósito da Matemática é ser uma forma de linguagem necessária para diversas ciências ou para o dia-a-dia dos indivíduos. Alguns defendem que ela é a verdadeira linguagem universal. Sem receio de cometer exageros, pode-se dizer também que a Matemática é uma das disciplinas escolares mais estudadas no mundo. Isso não implica que ela seja bem compreendida pela maior parte da população que a estuda. Por outro lado, mesmo sem compreender bem, as pessoas concordam com seus métodos e com seus critérios para o estabelecimento da Verdade. Muitas vezes, tais verdades parecem paradoxais, indo de encontro ao que se percebe por meio dos sentidos. Por exemplo, uma soma infinita de termos pode dar um número finito.
Com o método matemático, pode-se provar que algo existe ou é verdadeiro. Pode-se também provar que algo é falso. Mas em que consiste ou como funciona este método? Tentarei explicar rapidamente, sem me preocupar muito com as formalidades. O método matemático para provar que algo é verdadeiro (ou não) parte de premissas que são assumidas como “verdades primeiras”. Tais verdades são dogmáticas, ou seja, DEVEM ser aceitas. Elas são chamadas de postulados ou axiomas, sendo necessárias para que se possam provar “outras verdades”. Essas “outras verdades” são chamadas de teoremas. Os axiomas ou postulados são, muitas vezes, algo que pode parecer óbvio. Por exemplo, o 1º Postulado de Euclides[1] diz:
Uma linha reta sempre pode ser traçada entre dois pontos.
Qualquer indivíduo (que tenha estudado matemática) concordará com tal postulado. Isso porque poderá desenhar (ou imaginar) dois pontos e traçar uma linha reta passando por eles. Ele pode “ver” os conceitos do postulado e, facilmente, concordará. Acontece que o desenho do ponto não é o conceito ponto e sim uma representação de tal conceito. O conceito Ponto é uma invenção humana que sem a representação não poderia materializar-se, ou seja, é possível perceber um objeto que não existe na natureza por meio de uma representação. Tal objeto existe, porque foi definido. Trata-se de um exemplo de Definição Matemática. Euclides definiu Ponto como o que não tem partes, ou o que não tem grandeza alguma. A definição é também uma “verdade primeira”.
Os axiomas, postulados e definições, mesmo que pareçam óbvios, precisam ser formulados de maneira sistemática (os matemáticos gostam de falar em “Rigor Matemático”). Eles serão combinados com procedimentos lógicos para provar teoremas ou propriedades. Como exemplo, posso citar o famoso teorema de Pitágoras “Em todo triângulo retângulo, o quadrado da medida da hipotenusa é igual a soma dos quadrados das medidas dos catetos”. Provavelmente, o leitor deve ter aprendido[2] o teorema de Pitágoras como se fosse o “axioma” de Pitágoras. Todavia, trata-se de uma afirmação que precisou ser provada para ser considerada como uma verdade. Uma afirmação antes de ser provada é chamada de proposição. O procedimento para provar é chamado de “Demonstração Matemática” e usa axiomas, definições e outros teoremas já provados. Em geral, a elaboração de novos teoremas ocorre a partir de teoremas pré-existentes e não dos axiomas. Assim, para demonstrar bastaria usar teoremas anteriores que já foram provados, não sendo necessário explicitar axiomas ou definições já explicitadas nas provas desses teoremas. A proposição, uma vez provada, passa a ser considerada uma verdade inquestionável.
A prova de uma verdade matemática precisa valer para todos os casos em que aquela proposição está inserida. Ou seja, de alguma forma precisa ficar garantido que a verdade vale para todos os casos com aquelas características. É preciso atentar que não se demonstra que algo é verdade para todos, provando apenas em alguns casos. Por exemplo, é fácil verificar que num triângulo retângulo cuja hipotenusa mede 5cm e os catetos medem 3cm e 4cm é verdadeira a equação 5² = 4² + 3². Tal exemplo não garante que, para quaisquer valores da hipotenusa e catetos de um triângulo retângulo, a equação será verdadeira. Por outro lado, pode-se provar que algo não é uma verdade matemática a partir de um único contraexemplo! Ou seja, se exibirmos apenas um exemplo em que uma proposição não é válida, então isso é suficiente para dizer que a proposição não é verdadeira. Por exemplo, a proposição:
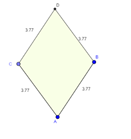
Todo quadrilátero que possui os lados com mesma medida é um quadrado.
Contraexemplo: A figura abaixo é um quadrilátero que possui todos os lados com mesma medida, mas não é quadrado, pois seus ângulos internos não medem 90º.
Existe também um método chamado de Demonstração por absurdo (ou contradição). Este tipo de prova[3] é feito assumindo-se como verdade o contrário do que queremos provar e então chegando-se a uma contradição. Por exemplo, consideremos a seguinte proposição:
Se um número b elevado a dois é par, então b é par.
Pode-se provar[4], por absurdo, que isso é uma verdade, mostrando que o contrário não pode existir, ou seja, assumindo que b é um número ímpar, efetuando alguns procedimentos e percebendo uma contradição lógica nas verdades que já foram provadas ou axiomas.
Existem proposições matemáticas que são provadas por um método que é chamado de indução matemática. De certa forma, ele tem relação com o método indutivo que é o raciocínio que, após considerar um número suficiente de casos particulares, conclui uma verdade geral. A indução[5], ao contrário da dedução, parte de dados particulares da experiência sensível. É importante destacar que o método de indução matemática parte de alguns casos particulares, mas não considera apenas eles para provar a proposição. Além disso, trata-se de um método limitado, não podendo ser usado para provar a maior parte das verdades matemáticas. Assim como o método indutivo não dá conta de provar a maior parte das verdades matemáticas, também não dá conta de provar outras verdades, sobretudo as que envolvem aspectos mais subjetivos. Acontece que, hoje em dia, é bastante comum vermos pessoas usando, inconsciente e equivocadamente, o método indutivo. A autoverdade parece se fundamentar equivocadamente nesse método.
Após esse breve contexto sobre como funciona o método matemático, pergunto: Seria possível propor um método parecido que pudesse auxiliar o debate sobre a meritocracia?
Poderíamos supor uma proposição:
A meritocracia é justa
Tal proposição, para ser considerada verdadeira, é preciso provar que ela é válida sempre e em todos os casos. Precisaríamos estabelecer algumas definições:
Meritocracia[6] é um sistema ou modelo de hierarquização e premiação baseado nos méritos pessoais de cada indivíduo.
Justo – algo que é correto. Se considerarmos como Justiça no sentido da imparcialidade, podemos considerar os seguintes sinônimos: equanimidade, imparcialidade, isenção ou neutralidade[7].
Mesmo existindo outras formas de definir tais conceitos, percebe-se que se tratam de definições que são consensuais e não parece haver muitas divergências quanto a elas. O mais difícil é propor axiomas “consensuais” que servirão de base para provar se a proposição é ou não verdadeira. Dessa forma, proponho os seguintes axiomas:
Axioma 1: A sociedade é heterogênea.
Tal afirmação parece óbvia, mas vou explicar a partir de definições:
Sociedade[8] é o conjunto de pessoas que compartilham propósitos, gostos, preocupações e costumes, e que interagem entre si constituindo uma comunidade.
Heterogênea[9] é sinônimo de plural, diverso ou diferente. Trata-se de um adjetivo que corresponde ao substantivo heterogeneidade. Afirmar que algo é heterogêneo significa um conjunto de elementos desiguais entre si.
Diante de tais definições, pode-se constatar que o axioma é óbvio, não tendo características de uma proposição que precisa ser provada, afinal trata-se de algo que é, de maneira geral, bastante perceptível pelos sentidos.
Axioma 2: Na sociedade existem algumas comunidades menos heterogêneas.
O segundo axioma também parece óbvio, mas era necessário explicitá-lo, porque o axioma 1 pode dar a entender que na sociedade que é heterogênea não há possibilidade de existir, em nenhum aspecto, grupos mais homogêneos.
Acredito que tais definições e axiomas são suficientes para provar se a proposição é ou não verdadeira.
Aqueles que acreditam que é verdadeira poderiam propor a prova em duas etapas:
1ª etapa: Pelo axioma 2, se existem comunidades menos heterogêneas, então existem pequenas desigualdades que não são determinantes para o sucesso ou fracasso do indivíduo. Logo, nesse conjunto a proposição é verdadeira.
2ª etapa: Considere o axioma 1 e o método indutivo. Existe o indivíduo “João” na sociedade heterogênea que, mesmo em situações desiguais (desfavoráveis), venceu pelo mérito individual. Como João e outros venceram, é possível generalizar da seguinte maneira: se foi possível com alguns, então é possível para todos. Basta repetir o que fizeram os indivíduos vitoriosos. Assim, a proposição é verdadeira também no conjunto em que as comunidades são mais heterogêneas.
Logo, para esses, a proposição seria verdadeira. Mas é possível contestar.
A 1ª etapa da prova parece correta. Não parece haver algum indício de erro lógico na argumentação. Já em relação à 2ª etapa não estou tão convencido. O principal erro parece estar em “então é possível para todos, basta repetir…”. O “basta” significa que é “suficiente”. Existem várias situações em que algo é necessário, mas não é suficiente. Simplesmente repetir o que os vitoriosos fizeram pode até ser uma condição necessária, mas não parece ser suficiente. Os que defendem que “basta repetir”, em geral, acreditam que apenas o “esforço” é suficiente. Todavia, podem-se usar contraexemplos para mostrar que essa tese está incorreta, pois existem muitos indivíduos que se esforçaram, tentando repetir as mesmas ações que levaram outros ao sucesso, mas não obtiveram êxito.
Portanto, tal prova não me parece ter conseguido mostrar que a proposição é verdadeira. Então ela seria falsa? O fato de não ter conseguido mostrar que é verdadeira, implica que a proposição seja falsa? Não! É preciso provar! Então é preciso provar que a “A meritocracia não é justa”. Isso pode ser escrito da seguinte maneira: “A meritocracia é injusta”.
Prova por absurdo:
Vamos supor a proposição “ A meritocracia é justa” e tentemos encontrar uma contradição.
Considerando justa no sentido de justiça[10], veremos que significa paridade, equidade, igualdade, isonomia, uniformidade. Então o fato de ser justa implica em que todos possuem condições iguais para conquistarem o sucesso. O axioma 1 diz que a sociedade é heterogênea e “heterogêneo significa um conjunto de elementos desiguais entre si.” Ora, o fato de existir elementos desiguais, naturalmente implica que as condições não podem ser completamente iguais. Assim, há uma contradição entre o axioma e a suposição “a meritocracia é justa”. Assim, a suposição é falsa e, portanto, a meritocracia é injusta. Mesmo em comunidades menos heterogêneas.
Diante do que foi visto, poderíamos questionar: Seria possível estabelecer condições para uma meritocracia justa? Um método meritocrático justo seria uma utopia? Qual seria a alternativa? Será que a solução não passa pela criação de ferramentas eficientes e justas para medir o mérito? Acho que estamos diante de um impasse que parece não ter solução, porque mesmo com as injustiças, a meritocracia parece ser ainda a única opção para decidir quem terá acesso a um conjunto limitado de coisas (certos bens, certas profissões etc). Por outro lado, acredito que a meritocracia em si não é o maior problema. O maior problema é usar a meritocracia como uma falácia, convencendo o indivíduo de que TODOS podem conseguir tudo por meio do mérito. Usar a meritocracia para justificar condições sub-humanas, convencendo o indivíduo de que se ele está numa vida ruim é por culpa de seu “demérito”! Mas o pior de tudo mesmo é usar a meritocracia como justificativa para ter privilégios que exploram o outro. Isso é o mais perverso!
É evidente que o método matemático não foi seguido à risca! Isso não seria possível, dadas às características do tema que estamos discutindo. Mas acredito ele foi útil para estabelecermos uma organização mais sistemática para o debate. Concluo dizendo que acho que é preciso estabelecer o AXIOMA PRIMEIRO que deveria ser a base para qualquer debate que envolve o bem comum. Para mim, tal axioma deveria ser: TODOS MERECEM A OPORTUNIDADE DE TER UMA VIDA DIGNA.
[1] https://pt.wikipedia.org/wiki/Os_Elementos
[2] Mais provável ainda é que tenha aprendido apenas a equação do teorema: a² = b² + c².
[3] https://pt.wikipedia.org/wiki/Prova_por_contradi%C3%A7%C3%A3o
[4] http://wiki.icmc.usp.br/images/7/72/Tiposdeprova.pdf
[5] https://pt.wikipedia.org/wiki/M%C3%A9todo_indutivo
[6] https://www.significados.com.br/meritocracia/
[7] https://www.sinonimos.com.br/justica/
[8] https://pt.wikipedia.org/wiki/Sociedade